Circle Inversi⊚n
20118 이도이
복소평면, 극좌표, 오일러 등식, 원반전
$\frac{1}{x}$
$\frac{1}{x}$
$$
\begin{align*}
&A = \{ x\ |\ 0 < x < 1,\ &x \in \R \} \\
&B=\{ x\ |\ 1 < x,\ &x \in \R \}
\end{align*}
$$
$$
\begin{align*}
&A = \{ x\ |\ 0 < x < 1,\ &x \in \R \} \\
&B=\{ x\ |\ 1 < x,\ &x \in \R \}
\end{align*}
$$
$$
\huge n(A) < n(B)\quad\text{?}
$$
$$
\begin{align*}
&A = \{ x\ |\ 0 < x < 1,\ &x \in \R \} \\
&B=\{ x\ |\ 1 < x,\ &x \in \R \}
\end{align*}
$$
$$
\huge n(A) = n(B)\quad\text{!}
$$
$\huge f: (0,\ 1) \rightarrow (1,\ \infty)$
$\huge f: (0,\ 1) \rightarrow (1,\ \infty)$
$\huge f(x) = \frac{1}{x}$
$\huge f(x) = \frac{1}{x}$
Complex Plane
Complex Plane
$z=x+yi$
Complex Plane
$z_0=1+2i$
Eul$e$r's Formula
$\huge e^{i\theta}=\cos\theta+i\sin\theta$
$\huge e^{i\theta}=\cos\theta+i\sin\theta$
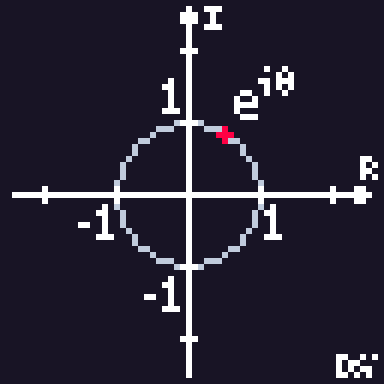
$\huge r\cdot e^{i\theta}=\cos\theta+i\sin\theta$
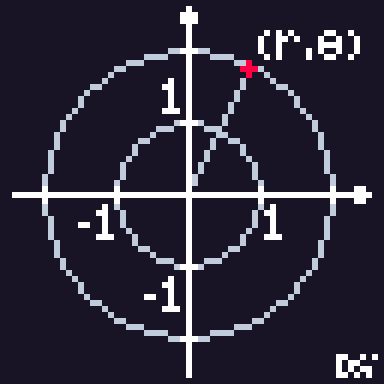
$\vec{P}$ola$r$ Coordinate
$\vec{P}$ola$r$ Coordinate
$(r,\ \theta)$
Complex $\vec{P}$ola$r$
$(r,\ \theta) \rightarrow r\cdot e^{i\theta}$
Gabriel's Horn
Gabriel's Horn
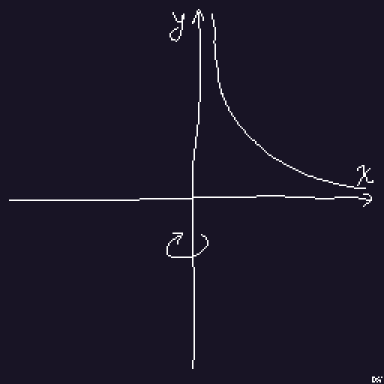
Gabriel's Horn
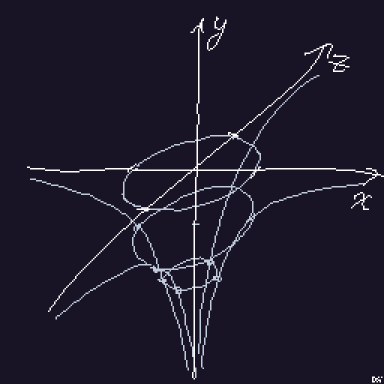
Gabriel's Horn
Circle Inversion
Circle Inversion
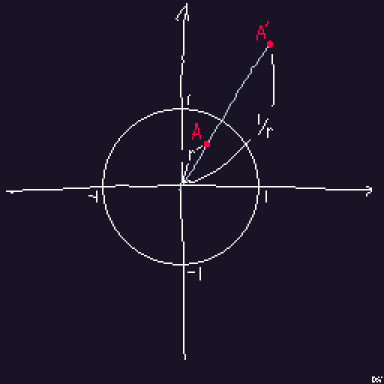$$
(r,\theta) \rightarrow (\frac{1}{r}, \theta)
$$
Circle Inversion
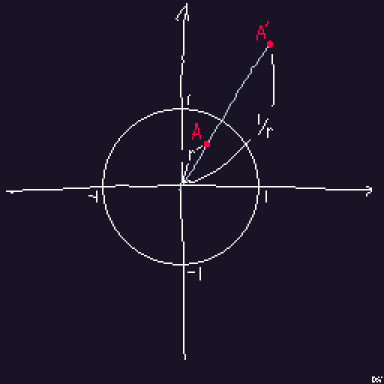$$
r\cdot e^{i\theta} \rightarrow \frac{1}{r}\cdot e^{i\theta}
$$
Circle Inversion
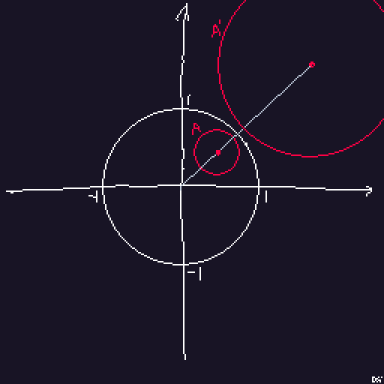
원반전된 원은 여전히 원이다.
Circle Inversion
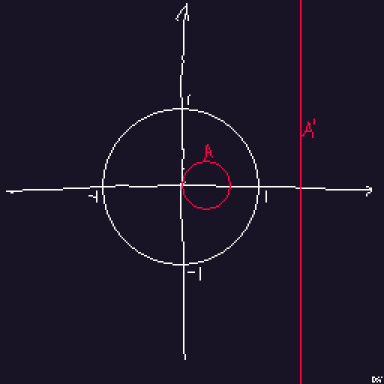
대상 원이 기준 원의 중심을 지날때,
반전된 원은 직선이 된다.